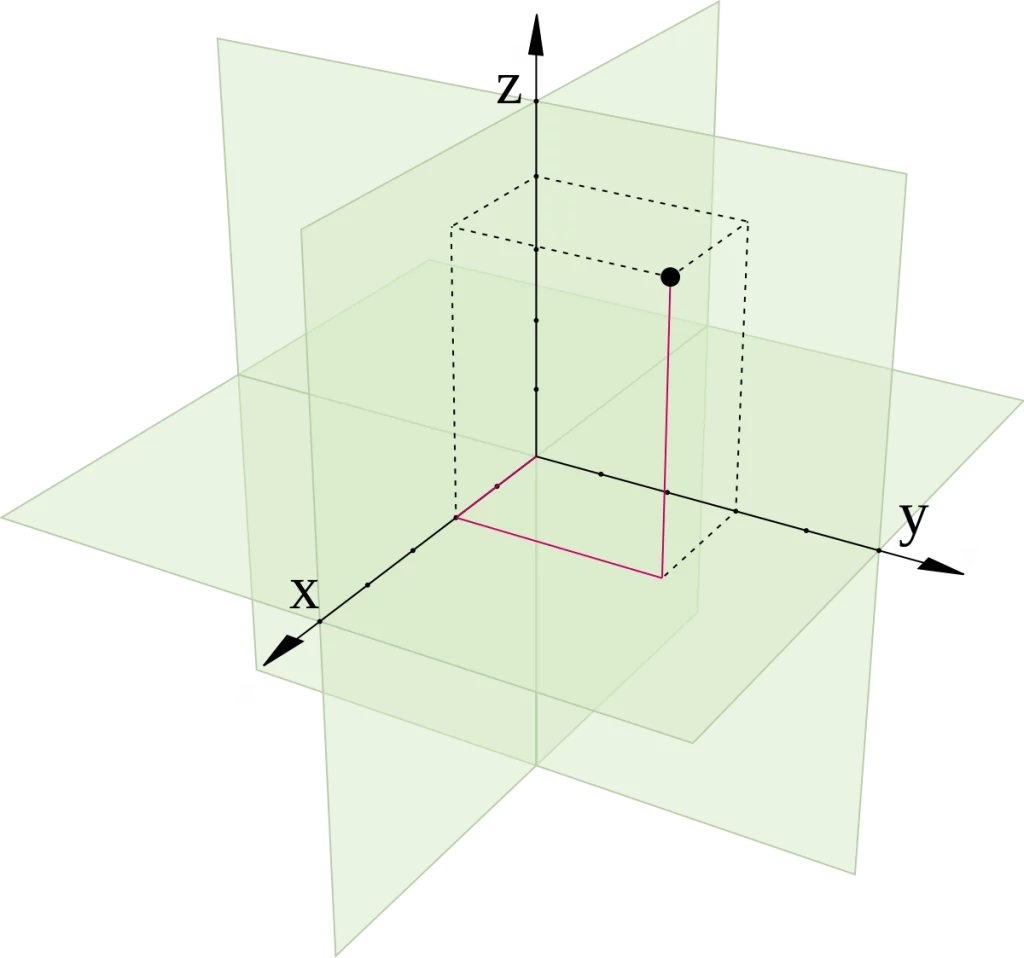
Espaços, Eixos e Planos

ESPAÇO BIDIMENSIONAL, TRIDIMENSIONAL E QUADRIDIMENSIONAL

O "espaço bidimensional" é formado por duas dimensões (altura e largura), sendo plano em sua essência. Ele é apenas um ente ideal (teórico), pois no mundo real, qualquer superfície palpável é formada pelo menos por três dimensões. Os entes primitivos do espaço bidimensional são o ponto e a linha (aqui entendida como uma sucessão retilínea e/ou curvilínea). São características do espaço bidimensional: a existência de um único plano infinito, a existência de infinitos pontos e retas (concorrentes e paralelas) por exemplo, e resolução de problemas que envolvem lugares geométricos, proporções, divisões, distâncias, intervalos, comprimentos, ângulos, áreas, representações de pontos, retas, linhas, polígonos, formas, ou sólidos por rebatimento e expressões.

O espaço tridimensional, de acordo com a linguística, é aquele que pode ser definido como tendo três dimensões (altura, profundidade e largura), o que na prática indica relevo. Os povos da Antiguidade trabalhavam com formas volumétricas, mas o estudo metódico do tema pode ser encontrado nos livros de Euclides que também trabalhava com o tridimensional quando estudava os sólidos (embora a geometria euclidiana se dedique a geometria plana que inclui o espaço euclidiano).

A geometria analítica tridimensional e a geometria descritiva trataram do espaço tridimensional de maneiras diferentes, mas com conteúdo aproximado, a primeira usou a linguagem algébrica e a segunda a geométrica.

Com o surgimento da terceira dimensão, alguns problemas geométricos que não existiam no bidimensional passaram a ser estudados, como:
Distância entre planos paralelos; Distância entre retas reversas; Cálculo de volumes; Elaboração de sistemas projetivos etc...

Um Octante em Geometria Espacial é uma das oito divisões de um Sistema de Coordenadas Tridimensional Euclidiano definido pelos sinais das coordenadas. O conceito é semelhante ao de quadrante do caso bidimensional e ao de semirreta unidimensional.
A generalização de um octante é chamada de ortante.

Nomenclatura e numeração:
Uma convenção de nomeação para os octantes é fornecer a lista dos seus sinais, ( + - - ) ou ( - + - ). O octante ( + + + ) às vezes é chamado de primeiro octante, apesar de não estarem definidas descrições ordinais semelhantes para os outros sete octantes. As vantagens de utilizar a notação ( + - - ) ou notações são a ausência de ambiguidade, e a sua extensibilidade para dimensões maiores.


Três planos axiais (x=0, y=0 e z=0) dividem o espaço em oito domínios octantes igual, cada um com um vetor de coordenadas entre ( -, -, -) e (+,+,+).

A Física Clássica Newtoniana baseia-se no espaço tridimensional. Como consequências teóricas têm-se:

  1. O espaço é absoluto

  2. o tempo é absoluto

  3. o movimento é absoluto

  4. intervalos de tempo são por toda a parte idênticos, sob todas as condições

  5. as dimensões dos corpos rígidos são independentes do estado de repouso ou movimento

  6. os axiomas de Euclides permanecem verdadeiros para todo Universo

  7. a gravitação é devida a uma atração entre os corpos

  8. raios de luz propagam-se em linha reta. Etc

Ambiente virtual tridimensional

Na informática, o "espaço virtual tridimensional" ou "ambiente virtual 3D", é um tipo de ambiente criado por técnicas computacionais, como a técnica realidade virtual (RV), na tentativa de simular um ambiente real, uma representação mais próxima do mundo real do que uma imagem com duas dimensões (altura e largura). É apresentado ao utilizador num dispositivo tecnológico um ambiente virtual em três dimensões que possui recursos que dão a ideia de profundidade onde o utilizador pode mover-se através dele passando uma sensação de presença real (simulação da realidade).

O espaço quadridimensional é o espaço formado por quatro dimensões: altura, largura, profundidade e, tempo.

Depois do surgir da Teoria da Relatividade de Albert Einstein, o espaço tridimensional foi revisto, pois a relatividade afirma que o espaço e o tempo compõem a bidimensão espaço-tempo, seguindo a fórmula anterior, ao espaço tridimensional foi acrescentado o tempo.

Em homenagem a Euclides, criou-se o termo espaço-tempo euclidiano, onde não há diferença entre direção no tempo e direção no espaço. O sistema geométrico criado por Euclides era bidimensional, contudo, o sistema bidimensional espaço-tempo citado, tem na realidade quatro dimensões.

“Isto basta. Newton, perdoe-me; Você encontrou o único meio, que na época, era o único possível para um homem do mais elevado pensamento e poder criativo. Os conceitos, que criou, estão até hoje guiando os nossos pensamentos em Física, embora nós agora saibamos que eles terão que ser substituídos por outros, removidos, mais além, da esfera da experiência imediata, se nós pretendemos uma compreensão mais profunda das relações”. - Albert Einstein

Propõe-se, cada vez mais, que os espaços da superfície terrestre sejam concebidos não como entidades tridimensionais, mas sim, quadridimensionais, como complexos de fenómenos espaço-temporais.

Depois da Teoria especial da relatividade (1905) e da Teoria geral da relatividade (1915), que abordava os efeitos referentes à gravidade, ocorreram as seguintes mudanças no pensamento científico, baseados na Física Relativista:


  1. o espaço e o tempo foram considerados dependentes (espaço-tempo contínuo)

  2. os corpos rígidos contraem-se na direção em que se movem

  3. as variações de medida do espaço e do tempo ocorrem de tal forma que a velocidade da luz permanece constante para todos os observadores

  4. o movimento retarda o relógio

  5. o campo de gravitação produz variações nas medidas do espaço-tempo, o intervalo entre dois factos é o mesmo para todos os observadores

  6. o campo de gravitação altera a natureza do espaço e encurvam os raios de luz

  7. o espaço-tempo contínuo produz uma geometria não-euclidiana

  8. para distâncias astronómicas, a menor distância entre dois pontos é uma curva













Criado por Anabela Pereira